算数問題34 直角三角形の辺の長さ
下図のような直角三角形 ABC があります。
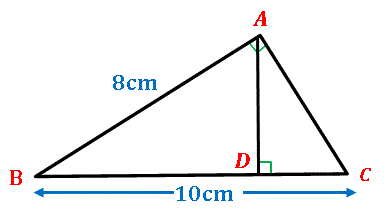
辺 AB の長さは 8 cm で、辺 BC の長さは 10 cm です。
頂点 A から辺 BC に垂直な線を引き、BC と交わる点を D とします。
辺 BD の長さを求めてください。
ヒント(似ているものが … )
「似ている」ものがありますよ。
解答(2つの角が等しい三角形は相似です)
△ABC と △ADB に注目します。
∠BAC と∠BDA はともに直角で、∠B も共通しています。
2つの角が等しい三角形は相似 なので、対応する辺の長さの比は等しく
BC:BA = BA:BD
という関係にあります。
10:8 = 8:BD
10:8 は 1:8/10 = 1:4/5 と書き直せるので、 8 に 4/5 をかけると BD の長さを求めることができます。
BD = 8 × 4/5 = 32/5 = 6.4 cm

エクセルや数学に関するコメントをお寄せください