定価で売れた商品はいくつ？

　前回の問題『大売出しで商品を捌きましょう！』 とペアになっている問題です。今回の問題では、前回問題の答えとなっている利益の合計などが最初から与えられていますが、定価で売れた数などが隠されています。隠されている数を変えるだけで、こうも難しさが変わってしまうというのが算数の面白さでもあります。

【算数問題25】売れ残った商品を1割引きで売りました

　南鬼久保（みなみおにくぼ）さんの店である商品を 200 個仕入れ、2 割の利益が出るように定価をつけて売り出しました。しかし商品は売れ残ってしまい、仕方なく定価の 1 割引で売って 1 個につき 64 円の利益で我慢しようと思いました。それで商品を全て売ることができ、利益の合計は 24320 円でした。定価で売れた商品 は何個ですか？

【ヒント】かなりの難問です。定価で売れた商品の個数以前に、とても重要な数値が欠けているので、まずその値を求めます。方程式を使うことを前提とした中学の数学問題だとしたら難しくないのですが、その手法が封じられると色々な工夫が必要になります。なるべく方程式を使わないで解いてみてください。

【解答】大切な情報は 仕入れ値 です。線分図を描いてみましょう。こういう問題では求める値を 1 とおく場合も多いのですけど、大抵の場合は 100 か 1000 とおいたほうが、あまり分数がでてこないので計算が楽になります。ここでは 仕入れ値を 100 とおくことにします。すると定価は

定価 = 仕入れ値 × 1.2 = 120

となりますね。この定価の 1 割を計算すると

定価の 1 割 = 120 × 0.1 = 12

です。このへんで図にしてみましょう。

　

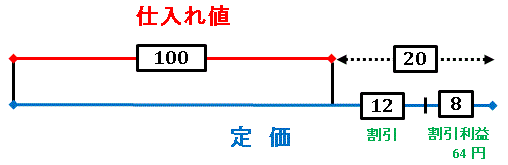
　図にあるように、定価から仕入れ値を差し引いた 20 のうち、12 が定価の 1 割、残りの 8 が割引で売った場合の利益です。これは問題で 64 円という具体的な値段が与えられていますね。あとは図をよく見て、比例関係から仕入れ値を求めます。青い線の一番右にある切れ端が「100 の中にいくつあるのかな？」と考えると

100 の中にある切れ端の個数 = 100/8 = 25/2

ですね。ちょっと分数が出てきて半端ですけど、「 12 個と半分あるね」とわかります。この切れ端 1 つが 64 円なのですから、上の個数をかけると仕入れ値を求めることができますね。

仕入れ値 = 切れ端の個数 × 64 = 25/2 × 64 = 800円

となって、ようやく仕入れ値を求めることができました！

　「何かもう、じゅうぶんに算数したなあ」という気分になりますが、これはまだまだ準備段階に過ぎません。ここからが本題です。定価で売ったときの利益を求めておきましょう。上の図を見ると

定価で売ったときの利益 = 仕入れ値 × 0.2 = 800 × 0.2 = 160円

ですね。最終的に求めたいのは 定価で売れた品物の個数 ですから、面積図を作って解いていきます。

　

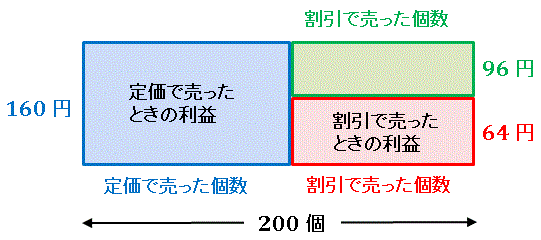
　青い長方形が定価で売ったときの利益、赤い長方形が割引で売ったときの利益です。縦の長さが 1 個あたりの利益、横の長さが商品の個数となっています。右上に緑の長方形を加えて大きな長方形を作ると、その面積は

大きな長方形の面積 = 160 × 200 = 32000

となりますね。そして赤い部分と青い部分を足した面積、つまり利益の合計は問題文で与えられています。

赤い長方形 + 青い長方形 = 24320

　大きな長方形から赤い長方形と青い長方形を差し引けば、緑の長方形が得られます。

大きな長方形の面積 - [赤い長方形 + 青い長方形] = 7600

　そして緑の長方形を縦の長さ 96 で割れば割引で売った個数が求められます。

割引で売った個数 = 7600/96 = 80個

　問われているのは定価で売れた個数ですから、

定価で売れた個数 = 200 - 80 = 120個

となるわけです！